Electronic spectra for T.Y B.Sc students Paper308

Paper- 308:  Inorganic Chemistry

Unit – I B :- Electronic Spectra

Syllabus Points

•      Electronic spectra of transition metal complexes.

•      Laporte orbital and spin selection rules.

•      Orgel energy level diagram of d⁵ and combined diagrams of d¹ - d⁹, d² – d⁸, d³ – d⁷, d⁴ – d⁶ and their spectra.

•      Jahn Teller distortion.

•      Spectrochemical series.

Electronic spectra of transition metal complexes:-

•      Electronic transitions between different energy containing orbitals gives spectra.

•      For such transition, Organic and Inorganic compounds required 1.5 x 10^-5 to 6 x 10⁵ jule/mol.

•      So the spectra is observed in visible or Ultra Violet region.

•      This kind of Spectra is called Electronic spectra.

Characteristics of Electronic Spectra:-

•      Position of crest of Spectra: - Indicate the measurement of the energy of the transition.

•      Intensity of spectra Є (Molar absorption constant):- Types of electronic transition can be calculated.

•      Shape of Band obtained in spectra:- Indicates the effect of electronic configuration of metal on spectra

•      Breadth of bands obtained in spectra: - Indicates effect of Ligand on Metal ion.

Selection rules for electronic transition:-

•      Intensity or height of electronic spectra is based on the probability of electronic transition.

•      If there is high probability of electronic transition, then more light is absorbed during transition, so the spectra which is obtained would be more intense and high.

•      There is two selection rules to decide allowed or forbidden transitions.

Spin selection rules (ΔS = 0):-

•      During the transition the total spin of molecule (atom or ion) should remain constant.

•      If ΔS ≠ 0, then such transition is forbidden.

•      If ΔS = 0, then such transition is allowed.

•      This rule is also known as rule of spin multiplicity.

•      According to this rule singlet → singlet, doublet → doublet, triplet → triplet are allowed transitions.

•      And singlet → triplet, doublet → quartet, doublet → triplet are forbidden transition.

Laporte orbital selection rules (Δl = ± 1):-

•      For Δl = ± 1 allowed transition, which gives sharp band.

•      For Δl ≠ ± 1 forbidden transition.

•      Each electron has finite value of its orbital angular quantum number l, and its orbital has definite symmetry too.

•      According to this rule s→p, p →s, p → d,d → p, d → f, f → d are Laporte allowed transitions which gives sharp band.

•      g → u and u → g are allowed transitions, while g → g, u → u are for bidden transition.

Orbital	l	symmetry
S	0	gerad
P	1	ungerad
D	2	gerad
f	3	ungerad

Intensity of different types of Electronic transitions:-

Type of transition	Approx. Є (Molar absorption constant)
Spin forbidden, Laporte forbidden	10-2 to 1.0
Spin allowed, Laporte forbidden	1 to 10
Spin allowed, Laporte forbidden (but p and d-orbitals overlaps)	10 to 102
Spin allowed, Laporte forbidden (intensity stilling effect)	102 to 103
Spin allowed, Laporte allowed	104 to 105

Characteristic of Bands of d-d transition:-

•      Bands of d-d transition are weaker:

•      Generally the frequency of electronic spectra is Є = 10⁴. But the frequency of d-d band is 0 to 100. It means d-d band is more weak.

•      According to crystal field theory, the symmetry of d-orbital is g (girad). So d-d transition means g → g transition which is Laporte’s forbidden.

•      According to crystal field theory, if molecule is completely symmetrical, then for d-d transition ΔL=0, so again it’s a Laporte’s forbidden transition and it can not give a band.

•      Here, d-d transition is for bidden yet transition is possible because according to crystal field theory,  in molecule complete symmetry will not remain due to some vibronic coupling, molecule get distorted so p and d-orbitals mix with each other which generate dissymmetry in the molecule so d-d transition  become possible.

•      This molecular dissymmetry  due to vibronic interaction in molecule is less so the transition which taken place is  also less. As a result of this less energy is absorbed so the bands which obtained are Weak

Bands of d-d transition are broad:-

•      Here levels of ground state and excited states of transition complex are not completely as crystal field theory.

•      Here electron spin and orbital coupled which raise Jahn teller effect, moreover due to vibration of ligand ground state as well as excited state split into many energy levels.

•      So instead of only one level less energy difference containing more transition take place.

•      As a result of that energy is continuously absorbed, so the band which obtained becomes BROAD.

•      For d¹ to d⁹ system, according to R-S coupling Spin-Orbital coupling of ²D term split into equivalent orbitals.

•      For ²T₂g term, spin-orbital coupling constant for Ti³⁺ and Cu²⁺ is 155cm^-1.

•      This value suggests that sharpness of band is not possible and as a result of this the band obtained is BROAD.

•      According to John teller effect, d-orbital lose its symmetry and split or distort.

•      So in d¹ and d⁹ system instead of only one transition less energy containing many transitions take place.

•      These transitions have less difference so instead of SHARP it gave BROAD band.

Vibronic coupling:-

•      According to laporte’s rule, d-d transition in complex compound is forbidden, so the band of such transition should not be obtained.

•      According to CFT, when d-orbital split in octahedral field then d-d transition become possible.

•      If the octahedral field of complex is not symmetrical then d and p-orbitals of complex overlaps (mixed) with each other and p-orbital’s character containing electron transit to d-orbitals.

•      As the extant of this overlapping is more, the band which obtained is more intense.

•      Generally in such transitions the value of Є is between 10 to 100.

•      If the octahedral field is symmetrical yet due to vibration of ligand present in complex, the octahedral field turns distorted.

•      During this asymmetric condition of complex d and p-orbitals get partially overlapped.

•      It results into transition of less frequency (Є ≈ 5-25)

•      Such transition is called Vibrational allowed transition and the phenomena Vibrational Coupling.

•      The frequency of obtained band is less and absorption  occurs from visible region so the complex having such transitions contain very fainted colour.

•      i.e.: [Mn(H₂O)₆]²⁺ complex have octahedral symmetry. But due to Vibrational coupling it contain pale Pink colour.

Identification of Oh- & Td- complexes through Electronic spectra:-

•      In absence of Ligand field all five d-orbitals of Metal are degenerate.

•      According to CFT, in octahedral and tetrahedral fields d-orbitals of metal ion split into two energy levels.

•      The energy difference between these splited levels for octahedral field is Δₒ and for tetrahedral field is Δt.

•      The value of Δt is less then Δₒ. It means   Δₒ ≈ Δt.

•      Here as the geometry of ligand field is changed, the splitting of d-orbital is changed, so the energy difference between splitted orbitals get changed.

•      Thus, as the ligand field in octahedral and tetrahedral fields is changed, the position of spectra, frequency and symmetry of band is changed.

•      The band in tetrahedral field is more intense then octahedral field.

•      In tetrahedral field absorption is more so it gives more intense colour.

•      In both the fields, the number of bands and their position are different.

i.e.: (i) [Mn(H₂O)₆]²⁺ and [MnBr₄]^2- complexes can be identified on the bases of their electronic spectra.

(ii) [Mn(H₂O)₆]²⁺ complex is octahedral which gives very pale pink colour while MnO₄^- is tetrahedral and contain intense violet colour.

According to Laporte’s rule d → d transition is forbidden, so all the transition complexes should be colour less but it is not true.

·         According to Laporte’s  rule d → d transition is forbidden so the band of such transition should not be obtained.

·         According to crystal field theory d orbitals split into octahedral field.

·         If octahedral-field of complex is not symmetrical, then its symmetry centre gets destroyed. So d and p orbitals of complex overlaps and transition of p-orbital character containing electron take place into d-orbital. The intensity (frequency)  of band (ϵ) is depended on the extent of overlapping. Generally in such transitions the value of ϵ is found between 10 to 100.

•       If the octahedral field is symmetrical yet due to vibration of ligand present in complex, the octahedral field turns distorted.

•      During this asymmetric condition of complex d and p-orbitals get partially overlapped.

•      It results into transition of less frequency (Є ≈ 5-25)

•      Such transition is called Vibrational allowed transition and the phenomena Vibrational Coupling.

•      The frequency of obtained band is less and absorption occurs from visible region so the complexes having such transitions contain much fainted colour.

•      i.e.: [Mn(H₂O)₆]²⁺ complex have octahedral symmetry. But due to Vibrational coupling it contain pale Pink colour.

Complexes of Zn²⁺ are mostly colourless:-

↑↓

↑↓

↑↓

↑↓

↑↓

·         Electronic configuration of Zn²⁺ is 3d¹⁰ 4s⁰ :

3d                                4s

·         Here all five d-orbitals are completely filled. The CFSE (Crystal Field Stabilization Energy) in the effect of octahedral field is zero. It means the value of Δₒ = 0. So d-orbital doesn’t split. Moreover there isn’t any vacant orbital left for d → d transition. As a result of this the complexes of Zn²⁺ is always colourless.

Electronic absorption bands of cis-MA₄B₂ is more instance then trans-MA₄B_2.

·         Symmetry centre ‘i’ exists in trans isomer. So d-orbitals are girad. In trans isomer     d → d transition band is on g → g. This kind of transition is Laporte forbidden (Δl ≠ ± 1) so their bands are weak.

·         There isn’t any symmetry centre ‘i’ in cis isomer. In this isomer the symmetry of d-orbital is more distorted then trans isomer. So the probability of d → d transition is more that is the reason that the electronic absorption bands of cis isomer is more intense then trans isomer.

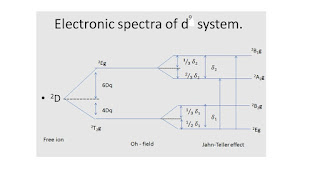
Electronic spectra of d¹-system:-

·         Ti³⁺ (Z = 22) : [Ar] 3d¹ 4s^o is a d¹ system. The term symbol is ²D.

·         In [Ti³⁺(H₂O)₆]³⁺, according to CFT (Crystal Field Theory) all five d-orbitals do not remain equivalent.

·         Due to octahedral field effect of H₂O ligand the degenerate d-orbitals of Ti³⁺ splits and produces two energy levels such as lower energetic ²T_2g (dxy, dyz, dxz) and higher energetic ²Eg (dx²-y², dz²) .

·         Thus according to CFT ²T_2g → ²E_g type of only one transition take-place and only one band should be obtained. But electronic spectrum of [Ti(H₂O)₆]³⁺  is of two bands, asymmetric and broad. This can be explained using John-teller theory.

·         According to John-teller theory, non-linear molecule containing equivalent orbitals gets distorted and in its ground state the degeneracy also destroyed. Thus [Ti(H₂O)₆]³⁺ molecule lost its symmetry according to John-teller’s effect and further split.

·         Thus instead of only one transition, the distorted octahedral field split and gives further three transitions : Instead of  ²T_2g ← ²E_g transition,

·         1) ²B_1g → ²E_g at 20,300 cm^-1,

·         2) ²A_1g ← ²E_g at 17,400 cm^-1,

·         3) ²B_2g ← ₂E_g the energy of this transition is very low and near IR region, so it is not found in visible region therefore only two bands are obtained.

·         The energy difference between transition 1 and 2 is very low, so their bands are obtained closer to each other as big peak along with a shoulder peak.

• Here levels of ground state and excited states of transition complex are not completely as crystal field theory.
• Here electron spin and orbital coupled which raise John-teller effect, moreover due to vibration of ligand ground state as well as excited state split into many energy levels.
• So instead of only one level less energy difference containing more transition take place.
• As a result of that energy is continuously absorbed, so the band which obtained becomes BROAD.
• For d¹  system, according to R-S coupling Spin-Orbital coupling of ²D term split into equivalent orbitals.
• For ²T₂g term, spin-orbital coupling constant for Ti³⁺  is 155cm^-1.
• This value suggests that sharpness of band is not possible and as a result of this the band obtained is BROAD.
• According to John teller effect, d-orbital lose its symmetry and split or distort.
• So in d¹ system instead of only one transition less energy containing many transitions take place.
• These transitions have less difference so instead of SHARP it gave BROAD band, so [Ti(H₂O)₆]³⁺ contain violet colour.

Application of the position of absorption band :-

Electronic spectra of d⁹-system:-

·         Cu²⁺ (Z = 29) : [Ar] 3d⁹ 4s^o is a d⁹ system. The term symbol is ²D.

·         In [Cu(H₂O)₆]²⁺, according to CFT (Crystal Field Theory) all five d-orbitals do not remain equivalent.

·         Due to octahedral field effect of H₂O ligand the degenerate d-orbitals of Cu²⁺ splits and produces two energy levels such as lower energetic ²T_2g (dxy, dyz, dxz) and higher energetic ²Eg (dx²-y², dz²) . Thus according to CFT, ²T_2g → ²E_g type of only one transition take-place and only one band should be obtained. But electronic spectrum of [Cu(H₂O)₆]²⁺  is of two bands, asymmetric and broad. This can be explained using John-teller theory. According to John-teller theory, non-linear molecule containing equivalent orbitals gets distorted and in its ground state the degeneracy also destroyed. Thus [Cu(H₂O)₆]²⁺ molecule lost its symmetry according to John-teller’s effect and further split. 

                                        Thus instead of only one transition, the distorted octahedral field split and gives further three transitions : Instead of  ²T_2g ← ²E_g transition,

·         1) ²B_1g → ²E_g 

·         2) ²A_1g ← ²E_g 

·         3) ²B_2g ← ₂E_g the energy of this transition is very low and near IR region, so it is not found in visible region therefore only two bands are obtained.

·         The energy difference between transition 1 and 2 is very low, so their bands are obtained closer to each other as big peak along with a shoulder peak.

• Here levels of ground state and excited states of transition complex are not completely as crystal field theory.
• Here electron spin and orbital coupled which raise John-teller effect, moreover due to vibration of ligand ground state as well as excited state split into many energy levels.
• So instead of only one level less energy difference containing more transition take place.
• As a result of that energy is continuously absorbed, so the band which obtained becomes BROAD.
• For d⁹  system, according to R-S coupling Spin-Orbital coupling of ²D term split into equivalent orbitals.
• For ²T₂g term, spin-orbital coupling constant for Cu²⁺  is 155cm^-1.
• This value suggests that sharpness of band is not possible and as a result of this the band obtained is BROAD.
• According to John teller effect, d-orbital lose its symmetry and split or distort.
• So in d⁹ system instead of only one transition less energy containing many transitions take place.
• These transitions have less difference so instead of SHARP it gave BROAD band, so [Cu(H₂O)₆]²⁺ contain blue-green colour.

               According to CFT of [Ti3+ (H2O)6]3+ the five d – orbitals of metal will not remain degenerate. Due to octahedral field of H2O ligand, degenerate d-orbitals of Ti3+ get splitted. It give rise to two energy levels. Among them 2T2g energy level is triply degenerate orbitals   (dxy, dyz, dxz), which is known as t2g orbitals. While in higher 2Eg energy level is doubly degenerate orbitals (dx2-y2, dz2), which is known as eg orbitals. Thus according to crystal field, only one transition is possible and that is 2T2g →2Eg so only one peak should be observed. But electronic spectrum of [Ti3+ (H2O)6]3+ shows two peaks, one broad peak and the other shoulder peak. According to Jahn – teller effect, degenerate orbitals containing non linear molecule, become free from degeneracy and get distorted. Due to this degeneracy of orbitals destroys in the ground state as well. Thus [Ti3+ (H2O)6]3+ molecule, lose its symmetry and its degenerate orbitals further get splited.

 

•Here the octahedral field of complex turns asymmetric and split into 2B1g, 2A1g, 2B2g, 3Eg. •Among these the term 3Eg become ground state term. So instead of 2T2g →2Eg transition in octahedral field, three transition will take place. 

•1) 2B1g ← 3Eg of energy  20300cm-1

•2) 2A1g ← 3Eg of  energy 17,400

•3) 2B2g ← 3Eg  of  Least energy such least that it can be found in near IR region, so it is not found in visible region spectra.

 

•Transition 1) and 2) have less energy difference between them so their bands obtained closer so it observed as a shoulder peak along with a big peak so the bend of such complex is broad and asymmetric. These transitions are d – d transitions which are forbidden according to Laporte rule, but due to the vibration of ligands, distortion raised in symmetry of complex and d – orbitals get splited  and probability of transition take place. The absorption through such transition (vibrational + electronic) is less, so weak band is obtained. Moreover, difference in energy levels of electrons keep changing with vibrations, so the absorbing energy is of less energy difference and continuous so the bands which obtained are broad. The absorption from these transition is in violet field of visible region so the complex of [Ti3+ (H2O)6]3+  contains violet colour.